Алгоритм работы интерпретатора Пролога
Рекурсивный алгоритм ответа на запрос G1,G2,...,Gm (список целей) следующий.
* Если список целей пуст - завершает работу успешно.
* Если список целей не пуст, продолжает работу, выполняя (описанную далее) операцию ПРОСМОТР.
* ПРОСМОТР: Просматривает предложения (º фразы, клаузы) программы от начала к концу до обнаружения первого предложения C, такого, что голова (левая часть) C унифицируема с первой целью G1. Если такого предложения обнаружить не удается, то работа заканчивается неуспехом.
Если C найдено и имеет вид
H :- B1, ..., Bn,
то переменные в C переименовываются, чтобы получить такой вариант C¢ предложения C, в котором нет общих переменных со списком G1,...Gm. Пусть C¢ - это
H¢ :- B1¢ , ..., Bn¢ .
Унифицируется G1 с H¢; пусть S - результирующая конкретизация переменных. В списке целей G1, G2, ...,Gm, цель G1 заменяется списком B1¢,..., Bn¢, что порождает новый список целей:
B1¢, ..., Bn¢, G2, ..., Gm.
(Заметим, что, если C - факт, тогда n=0, и в этом случае новый список целей оказывается короче, нежели исходный; такое уменьшение списка целей может в определенных случаях превратить его в пустой, а, следовательно, - привести к успешному завершению.)
Переменные в новом списке целей заменяются новыми значениями, как это предписывает конкретизация S, что порождает еще один список целей
B1¢¢, ..., Bn¢¢, G2¢, ... , Gm¢.
* Вычисляется (используя тот же самый алгоритм) этот новый список целей. Если его вычисление завершается успешно, то и вычисление исходного списка целей тоже завершается успешно.
Если же его вычисление порождает неуспех, тогда новый список целей отбрасывается и происходит возврат (бэктрекинг) к просмотру программы. Этот просмотр продолжается, начиная с предложения, непосредственно следующего за предложением C (C - предложение, использовавшееся последним) и делается попытка достичь успешного завершения с помощью другого предложения.
Вычисление целей интерпретатор Пролога осуществляет с помощью поиска в глубину с возвратом
(в дереве целей): правило вычислений всегда выбирает первую слева подцель в текущем списке целей, а правило поиска выбирает из программы первую клаузу, голова которой унифицируема с данной подцелью. Если вычисление заходит в тупик, т.е. ни одно из утверждений программы не применимо к текущему списку целей, то происходит возврат назад по построенной ветви и для предыдущего состояния пробуется первое из еще не применявшихся к нему утверждений программы.
3. СЕМАНТИКА ПРОЛОГА
Арифметика в Прологе
Арифметические выражения
Простейшие операнды в арифметических выражениях:
* переменные,
* числа,
* вызовы арифметических функций,
* атомы.
Сложные арифметические выражения конструируются из операндов, круглых скобок и знаков операций.
Знаки операций:
унарные + , -
+ , - , * , /
// - целочисленное деление
mod - остаток от деления
^ - возведение в степень
Арифметические функции:
abs(X)
max(X,Y)
min(X,Y)
random(N) => 0£ i £ N (N,i - целые)
integer(X) - округление X до ближайшего целого
floor(R) => N (N£ R<N+1, пол - наибольшее целое £ R)
ceil(R) => N (N-1 < R £ N, потолок - наименьшее целое ³ R)
sqrt(X)
sin(X) - углы в радианах
cos(X)
tan(X)
asin(X)
acos(X)
atan(X)
log(X) º ln X
log10 (X)
exp(X) º e^X
pi =3.14159265358
e = 2.718281828459045
Описание предикатов. Используются следующие соглашения при описании предикатов в дальнейшем тексте (то же самое действует в help'е).
predicate(+A,-A,?A).
+ - входной аргумент
- - выходной аргумент
? - входной или выходной
Шаблон указывает возможные способы вызова предиката. Арность предиката указывается следующим образом:
predicate/3 - предикат с местностью (арностью) 3
Встроенные арифметические предикаты
Арифметические выражения вычисляются только тогда, когда они служат аргументами одного из встроенных арифметических предикатов.
=(?A,?B) , ?A = ? B - унификация термов A и B
?- X=3.
X = 3
Yes
?- X= 3+5.
X = 3 + 5
Yes
?- 3 = 1+2.
No
?- X = a+b.
X = a + b
Yes
is(-Number, +Expr) , -Number is +Expr
- детерминированный предикат (дает один ответ)
?- 5 is 2+(8 // 2).
No
?- 5 is (2+8) // 2.
Yes
?- X is 2*3,Y is 2^X.
X = 6
Y = 64
Yes
?- A is a+b. => ошибка
Предикаты сравнения чисел
+Expr1 > +Expr2 или >(+Expr1,+Expr2)
+Expr1 < +Expr2
+Expr1 =< +Expr2
+Expr1 >= +Expr2
+Expr1 =:= +Expr2 (равно)
+Expr1 =\= +Expr2 (не равно)
Программирование числовых функций
Предикат f(+N,?R) истинен тогда и только тогда, когда R равно факториалу натурального числа N, т.е. N! = R (= 1´2´…´N).
f(0,1).
f(X,Y):-
X > 0,
X1 is X -1,
f(X1,Y1),
Y is X*Y1.
Программирование с накапливающим параметром позволяет писать эффективные рекурсивные программы.
f1(N,N,R,R).
f1(N,X,Y,R):-
X =\= N,
X1 is X+1,
Y1 is Y*X1,
f1(N,X1,Y1,R).
f(N,R):-
f1(N,0,1,R).
Здесь второй параметр накапливает значение аргумента, третий – текущее значение факториала.
Лисп и Пролог основаны на рекурсии, поэтому есть некоторое сходство в стиле программирования. Основное отличие в том, что в функциональном программировании значение функции определяется в виде выражения, а на Прологе это выражение задается в виде терма, являющегося одним из аргументов предиката. Это похоже на различие между двумя способами возвращения результата процедуры. Его можно присвоить имени функции, а можно присвоить параметру - результату процедуры или подпрограммы. Второе главное отличие состоит в использовании предикатов в качестве “охраняющих условий” в начале дизъюнктов вместо условных выражений.
Декларативная и процедурная семантики
Декларативная семантика
программы касается только отношений, определенных в программе. Таким образом, декларативная семантика определяет, что должно быть результатом работы программы. Является ли целевое утверждение истинным, исходя из данной программы, и если оно истинно, то для какой конкретизации переменных.
Процедурная семантика Пролога - это процедура достижения списка целей в контексте данной программы. Процедура выдает истинность или ложность списка целей и соответствующую конкретизацию переменных. Процедура осуществляет автоматический возврат для перебора различных вариантов.
Декларативная семантика программы на “чистом” Прологе не зависит от порядка предложений и от порядка целей в предложениях.
Процедурная семантика существенно зависит от порядка целей и предложений. Поэтому порядок может повлиять на эффективность программы; неудачный порядок может даже привести к бесконечным рекурсивным вызовам.
Имея декларативно правильную программу, можно улучшить ее эффективность путем изменения порядка предложений и целей при сохранении ее декларативной правильности. Переупорядочивание один из методов предотвращения зацикливания.
Кроме переупорядочивания существуют и другие, более общие методы предотвращения зацикливания, способствующие получению процедурно правильных программ.
Определение – это попытка окружить пустыню стеной из слов.
Сэмюэль Батлер 1835-1902
Добавление элемента списку, если он отсутствует (добавление без дублирования)
добавить(X, L, L):-
member(X, L),!.
добавить(X, L, [X|L]).
?- добавить(5, [4, 3, 5], L).
L= [4,3,5];
No
?- добавить(5,[4,3],L).
L=[5,4,3];
No
Если убрать отсечение:
?- добавить (5, [4, 3, 5], L).
L = [4, 3, 5] ;
L=[5, 4, 3, 5];
No
Границы моего языка означают границы моего мира.
Людвиг Витгенштейн
Доступ к программам и обработка программ
clause(?Head, ?Body)
Успех, когда Head может быть унифицирована с головой клаузы и Body с соответствующим телом клаузы. Выдает альтернативные клаузы при бэктрекинге (поиске с возвратом). Для фактов Body унифицируется с атомом true. Обычно clause/2 используется для нахождения определения предиката, но может также использоваться для нахождения головы клаузы при некотором заданном образце тела.
?- clause(member(X,Y),Body).
Body = true
X = G904
Y = [G904|G1336] ;
Body = member(G904, G1348)
X = G904
Y = [G1344|G1348] ;
No
Существуют системные предикаты, выполняющие добавление предложений к программе и удаление предложений из программы.
assert(+Term)
Добавляет факт или правило в программу (в базу данных в оперативной памяти). Term добавляется как последний факт или правило соответствующего предиката.
Например, решение цели
?- assert(father(tom, bob)).
добавляет в программу факт father. При добавлении правил следует вводить дополнительные скобки, чтобы учитывать старшинство термов. Например, синтаксически правильным является выражение
?- assert((parent(X,Y):-father(X,Y))).
Имеется вариант предиката assert, а именно, asserta, добавляющий предложение в начало процедуры.
retract(+Term). Когда терм Term унифицируется с первым подходящим фактом или клаузой в базе данных, факт или клауза удаляется из базы данных.
retractall(+Term). Удаляются все факты или клаузы в базе данных, что унифицируются с Term.
Пролог-программу можно рассматривать как реляционную базу данных: описание отношений частично присутствует в ней в явном виде (факты), а частично в неявном (правила). Встроенные предикаты assert и retract дают возможность корректировать эту базу данных в процессе выполнения программ.
% программа о погоде
хорошая:-
солнечно,
not дождь.
необычная :-
солнечно,
дождь.
отвратительная :-
дождь,
туман.
дождь.
туман.
?- хорошая.
no
?- отвратительная.
yes
?- retract(туман).
yes
?- отвратительная.
no
?- assert(солнечно).
yes
?- необычная.
yes
?- retract(дождь).
yes
?- хорошая.
yes
Фразы Хорна как средство представления знания
Решение задач. Конечной целью составления компьютерной программы является создание инструмента, предназначенного для решения задачи из некоторой прикладной области. Прикладная область - это некоторая абстрактная часть мира или область знаний. Структура прикладной области состоит из значимых для этой области сущностей, функций и отношений. В удачной компьютерной программе структура прикладной области моделируется таким образом, что поведение этой программы во время выполнения будет отражать какие-то существенные аспекты данной структуры. К примеру, отношение, существующее между некоторыми сущностями прикладной области, должно, по аналогии, соблюдаться и для обозначений, которые представляют эти сущности в программе, моделирующей эту область.
Программирование. Процесс составления программы на Прологе в основном сходен с процессом построения теории в логике предикатов.
1) Программист анализирует значимые сущности, функции и отношения из прикладной области и выбирает обозначения для них.
2) Программист семантически определяет каждую значимую функцию и каждое значимое отношение. Для отношений указывается, какие конкретные их реализации дают истину, а какие - ложь.
3) Программист аксиоматически определяет каждое отношение при помощи фраз Пролога. Аксиоматическое определение отношения будет удачным, если оно отразит смысл семантического определения. Множеством аксиоматических определений всех значимых для заданной предметной области отношений является программа, моделирующая структуру этой области.
4) Для выполнения запросов к множеству фраз программист или пользователь применяет интерпретатор языка Пролог. Совокупность, состоящую из запроса, множества фраз программы и интерпретатора языка можно рассматривать как алгоритм решения задач из прикладной области. При этом запрос и фразы программы представляют собой начальные формулы алгоритма, а интерпретатор содержит правила преобразования этих формул. Интерпретатор играет роль активной силы, которая выполняет выводы из фраз программы и тем самым реализует
или развертывает отношения определенными фразами программы.
Р. Ковальский описывает сущность логического программирования фразой:
Алгоритм = Логика + Управление.
И поэтому в логике никогда не может быть ничего неожиданного.
Людвиг Витгенштейн
Информирует систему, что указанный
7.2. Ввод и вывод
Файлы являются последовательными. Существуют текущие входной и выходной потоки. Пользовательский терминал рассматривается как файл с именем user.
Переключение между потоками осуществляется с помощью процедур:
see (Файл) - файл становится текущим входным потоком;
tell (Файл) - файл становится текущим выходным потоком;
seen - закрывается текущий входной поток;
told - закрывается текущий выходной поток.
Файлы читаются и записываются двумя способами:
* как последовательности символов;
* как последовательности термов.
Встроенные процедуры для чтения и записи символов и термов таковы:
read(-Term) - вводит следующий терм;
write(+Term) - выводит Term;
put(+Char) - выводит символ, Char должно быть целочисленное выражение, значение которого есть код ASCII или атом в виде одной литеры;
get0(-КодСимвола) - вводит следующий символ;
get(-КодСимвола) - вводит ближайший следующий “печатаемый” символ.
Пример. Пусть во время работы создана база данных, состоящая из множества фактов вида father(X,Y). Требуется записать все эти факты в файл base.dat.
'записать базу данных':-
tell('base.dat'),
base,
told.
base:-
father(X,Y),
write(father(X,Y)),
write('.'),nl,
fail.
base.
7.3. Работа с базой данных “Достопримечательности”
(программа, которая учится у пользователя)
Предикат place(Место, Авеню, Стрит) связывает название места в городе с номерами улиц (авеню и стрит), на пересечение которых это место расположено. По заданному названию места данная процедура пытается определить его адрес, просматривая базу данных “адрес” (множество фактов вида adress(whitehous,7,1)). Процедура place действует с предположением об открытости мира в том смысле, что она не просто завершается неудачей, если не может найти название места в базе данных.
Вместо этого процедура переключается на другую стратегию и получает сведения от пользователя, выступающего в роли альтернативного источника знаний. Процедура place учится на своем опыте, добавляя новые ответы в текущую программу.
Эта программа работает следующим образом.
?- goal.
adress.dat compiled, 0.00 sec, 268 bytes. % загружается база данных
Введите название достопримечательности
whitehous.
Это место вблизи 7 авеню и 1 стрит.
Продолжать? yes
Введите название достопримечательности
grand_central.
-- это место - grand_central
вблизи какой авеню? (номер) 42.
вблизи какой стрит? (номер) 8.
Это место вблизи 42 авеню и 8 стрит.
Продолжать? yes
Введите название достопримечательности
grand_central.
Это место вблизи 42 авеню и 8 стрит.
Продолжать? no % записывается новая база данных в файл
Yes
Заметьте, что при выполнении второго запроса система спросила у пользователя адрес “grand_central”. Пользователь ввел 42 и 8, а затем интерпретатор вывел эти же самые значения как ответы на запрос. Если дать тот же запрос повторно, то процедура place уже будет знать адрес “grand_central”.
place(X,Avenu,Street) :-
adress(X,Avenu,Street),!.
place(X,Avenu,Street) :-
write('-- это место - '),write(X),nl,
write('вблизи какой авеню? (номер) '),
read(Avenu),
write('вблизи какой стрит? (номер) '),
read(Street),
assert(adress(X,Avenu,Street)).
run(X) :-
place(X,Avenu,Street),
write('Это место вблизи '),write(Avenu),write(' авеню'),nl,
write('и '),write(Street),write(' стрит.').
'ввести базу знаний' :-
consult('adress.dat').
goal:-
write('Спрашивайте:'),nl,
'ввести базу знаний',
repeat,
write('Введите название достопримечательности'),nl,
read(X),
run(X),nl,
'продолжать'.
'продолжать':-
write('Продолжать? '), yes.
yes:-
get_single_char(C),
(name(n,[C]),write('no'),'записать базу данных',!;
write('yes'),nl,fail).
'записать базу данных':-
tell('adress.dat'),
base,
told.
base:-
adress(X,Avenu,Street),
write(adress(X,Avenu,Street)),
write('.'),nl,
fail.
base.
История
Идея использования языка логики предикатов первого порядка в качестве языка программирования возникла еще в 60-ые годы, когда создавались многочисленные системы автоматического доказательства теорем и основанные на них вопросно-ответные системы. Суть этой идеи заключается в том, чтобы программист не указывал машине последовательность шагов, ведущих к решению задачи, как это делается во всех процедурных языках программирования, а описывал на логическом языке свойства интересующей его области, иначе говоря, описывал мир своей задачи. Другие свойства и удовлетворяющие им объекты машина находила бы сама путем построения логического вывода. (В сущности, этот же подход реализуется и в функциональном программировании - лишь с тем уточнением, что речь в нем идет о свойствах функций. В связи с этим Дж. Робинсон предлагает назвать такой стиль программирования утвердительным).
Первые компьютерные реализации систем автоматического доказательства теорем появились в конце 50-х годов, а в 1965г. Робинсон предложил свой метод резолюций, который и по сей день лежит в основе большинства систем поиска логического вывода.
Робинсон пришел к заключению, что правила вывода, которые следует применять при автоматизации процесса доказательства при помощи компьютера, не обязательно должны совпадать с правилами вывода, используемыми человеком. Он обнаружил, что общепринятые правила вывода, например, правило modus ponens, специально сделаны “слабыми”, чтобы человек мог интуитивно проследить за каждым шагом процедуры доказательства. Правило резолюции более сильное, оно трудно поддается восприятию человеком, но эффективно реализуется на компьютере.
К концу 60-х годов выявились принципиальные трудности, препятствующие широкому применению таких систем. Главная проблема заключается в практической неэффективности известных методов построения логического вывода. Стремление обойти эту преграду привело к созданию различных линейных стратегий метода резолюций (в том числе стратегии SL-резолюции), которые, в сущности, являются прообразами современных интерпретаторов языка Пролог. В 1971г. один из авторов SL-резолюции Р. Ковальский прочитал несколько лекций по автоматическому доказательству теорем в лаборатории Искусственного интеллекта Марсельского университета. Работающий там А. Колмероэ и его коллеги вскоре поняли, каким образом можно использовать SL-резолюцию в качестве основы нового языка программирования. Так в 1972 году родился язык Пролог (“ПРОграммирование в терминах ЛОГики”), быстро завоевавший популярность во всем мире.
Терпеть не могу логики. Она всегда банальна и нередко убедительна.
Оскар Уайльд
Эквивалентность программ и данных
Характерной особенностью Пролога является эквивалентность программ и данных - и то и другое может быть представлено логическими термами. Для того, чтобы можно было использовать эту эквивалентность, необходимо, чтобы программы можно было рассматривать в качестве данных, а данные можно было бы превращать в программы.
Смысл предиката call(X) в Прологе состоит в передаче терма X в качестве цели. Доступность метапеременных означает, что в качестве целей в конъюнктивных вопросах и в теле предложений разрешается использовать переменные. В процессе вычисления в момент обращения к такой переменной ей должно быть сопоставлено значение - терм. Если переменной не сопоставлено значение в момент обращения, то возникает ошибочная ситуация.
Вместо вызова предиката call(X) можно писать просто X.
Доступность метапеременных является важным инструментом метапрограммирования, используемым, в частности, при построении метапрограмм, которые обращаются с другими программами как с данными; они выполняют их анализ, преобразование и моделирование. Это же свойство существенно используется при определении отрицания и при определении предикатов высших порядков.
Пример: Определение отрицания.
not X :- X,!, fail.
not X.
Обладаю ли я знаниями? Нет. Но когда низкий человек спросит меня о чем-либо, то, даже если я не буду ничего знать, смогу рассмотреть этот вопрос с двух сторон и обо всем рассказать ему.
Конфуций
Этот вызов приводит к бесконечному циклу
?- pred3(lis,jim)
==> бесконечный цикл
Логический вывод
Проблема доказательства в логике состоит в нахождении доказательства формулы B (заключения), если предполагается истинность формул A1,...,An (посылок). Мы записываем это в виде
A1,A2,...,An |= B.
Основной метод решения этой проблемы следующий. Записываем посылки и применяем правила вывода, чтобы получить из них другие истинные формулы. Из этих формул и исходных посылок выводим последующие формулы и продолжаем этот процесс до тех пор, пока не будет получено нужное заключение. Мы называем это выводом; именно такой метод обычно применяется в математических доказательствах.
Посмотрим, как это делается.
Два классических правила вывода были открыты очень давно. Одно из них носит латинское название modus ponens (модус поненс или сокращение посылки). Его можно записать следующим образом:
A, A Þ B |= B.
Второе правило (цепное) позволяет вывести новую импликацию из двух данных импликаций. Можно записать его следующим образом:
A Þ B, B Þ C |= A Þ C.
Доказательство с введением допущения. В этом и следующих разделах речь пойдет о трех стратегиях доказательства. Первая называется введения допущения. Для доказательства импликации вида A Þ B допускается, что левая часть A истинна, т.е. A принимается в качестве дополнительной посылки, и делаются попытки доказать правую часть, B.
Этот метод часто применяется в геометрии. Например, при доказательстве равенства боковых сторон треугольника, у которого углы при основании равны, допускается, что эти углы равны, а затем это используется в доказательстве равенства сторон.
Приведение к противоречию. При построении выводов не всегда целесообразно ждать появления искомого заключения, просто применяя правила вывода. Именно такое часто случается, когда мы делаем допущение B для доказательства импликации B Þ C. Мы применяем цепное правило и модус поненс к B и другим посылкам, чтобы в конце получить C. Однако можно пойти по неправильному пути, и тогда будет доказано много предложений, большинство из которых не имеет отношения к нашей цели.
Этот метод носит название прямой волны и имеет тенденцию порождать лавину промежуточных результатов, если его запрограммировать для компьютера и не ограничить глубину.
Другая возможность - использовать одну из приведенных выше эквивалентностей и попытаться, например, доказать ØC Þ ØB вместо BÞC. Тогда мы допустим ØC и попробуем доказать ØB. Иными словами, допускается, что заключение C (правая часть исходной импликации) неверно, и делается попытка опровергнуть посылку B. Это позволяет двигаться как бы назад от конца к началу, применяя правила так, что старое заключение играет роль посылки. Такая организация поиска может лучше показать, какие результаты имеют отношение к делу. Она называется поиском от цели.
Можно использовать также комбинацию этих методов, называемую приведением к противоречию. В этом случае для доказательства B Þ C мы допускаем одновременно B и ØC, т.е. предполагаем, что заключение ложно:
Ø(BÞC) = Ø(ØBÚC) = B Ù ØC.
Теперь мы можем двигаться и вперед от B, и назад от ØC. Если C выводимо из B, то, допустив B, мы доказали бы C. Поэтому, допустив ØC, мы получим противоречие. Если же мы выведем ØB из ØC, то тем самым получим противоречие с B. В общем случае мы можем действовать с обоих концов, выводя некоторое предложение P, двигаясь вперед, и его отрицание ØP, двигаясь назад. В случае удачи это доказывает, что наши посылки несовместимы
или противоречивы. Отсюда мы выводим, что дополнительная посылка BÙØC должна быть ложна, а значит противоположное ей утверждение BÞC истинно. Метод приведения к противоречию часто используется в математике. Например, в геометрии мы можем допустить, что углы при основании некоторого треугольника равны, а противолежащие стороны не равны, и попробовать показать, что при этом и углы должны быть не равны, или получить еще какое-то противоречие.
Доказательство методом резолюции. Правило резолюции следующее: XÚA, YÚØA |= XÚY.
Оно позволяет нам соединить две формулы, удалив из одной атом A, а из другой ØA. Сравним это правило с уже известными нам:
цепное правило: ØX Þ A, A Þ Y |= ØX Þ Y,
модус поненс: A, AÞY |= Y.
Правило резолюции можно рассматривать как аналог цепного правила в применении к формулам, находящимся в конъюнктивной нормальной форме. Правило модус поненс также можно считать частным случаем правила резолюции для случая ложного X.
Чтобы применить правило резолюции, будем действовать следующим образом. Используем доказательство от противного и допускаем отрицание заключения.
1. Приводим все посылки и отрицание заключения, принятое в качестве дополнительной посылки, к конъюнктивной нормальной форме.
а) Устраняем символы Þ и Û с помощью эквивалентностей
AÛB = (AÞB)Ù(BÞA),
AÞB = ØAÚB.
б) Продвигаем отрицания внутрь с помощью закона де Моргана.
в) Применяем дистрибутивность AÚ(BÚC) = (AÚB)Ù(AÚC).
2. Теперь каждая посылка превратилась в конъюнкцию дизъюнктов, может быть, одночленную. Выписываем каждый дизъюнкт с новой строки; все дизъюнкты истинны, так как конъюнкция истинна по предположению.
3. Каждый дизъюнкт - это дизъюнкция (возможно, одночленная), состоящая из предложений и отрицаний предложений. Именно к ним применим метод резолюций. Берем любые два дизъюнкта, содержащие один и тот же атом, но с противоположными знаками, например,
XÚYÚZÚØP,
XÚPÚW.
Применяем правило резолюции и получаем XÚYÚZÚW.
4. Продолжаем этот процесс, пока не получится P и ØP для некоторого атома P. Применяя резолюцию и к ним, получим пустой дизъюнкт, выражающий противоречие, что завершает доказательство от противного.
В качестве примера рассмотрим доказательство соотношения
PÚQ,PÞR,QÞS |= RÚS.
Приводим посылки к нормальной форме и выписываем их на отдельных строках.
|
PÚQ |
(1) |
|
ØPÚR |
(2) |
|
ØQÚS |
(3) |
Ø(RÚS) = ØRÙØS
|
ØR |
(4) |
|
ØS |
(5) |
|
ØP из (2) и (4) |
(6) |
|
Q из (1) и (6) |
(7) |
|
ØQ из (3) и (5) |
(8) |
|
пустой из (7) и (8) |
- это позитивная или негативная атомарная формула. Каждая фраза (или клауза) - это множество литералов, соединенных символом Ú. Фразу можно рассматривать как обобщение понятия импликации. Если A и B - атомарные формулы, то формула
AÞB
может также быть записана как
B Ú ØA.
Простейшая фраза содержит только один литерал, позитивный или негативный.
Фраза с одним позитивным литералом называется фразой (или клаузой) Хорна.
Любая фраза Хорна представляет импликацию: так, например,
D Ú ØF Ú ØE равносильно FÙE Þ D.
Правило резолюции действует следующим образом. Две фразы могут быть резольвированы друг с другом, если одна из них содержит позитивный литерал, а другая - соответствующий негативный литерал с одним и тем же обозначением предиката и одинаковым количеством аргументов, и если аргументы обоих литералов могут быть унифицированы (т.е. согласованы) друг с другом. Рассмотрим две фразы:
|
P(a) Ú ØQ(b,c), |
(1) |
|
Q(b,c) Ú ØR(b,c). |
(2) |
В результате этого получается фраза (3), которая называется резольвентой:
|
P(a) Ú ØR(b,c). |
(3) |
|
P(a) Ú ØQ(b,c), |
(4) |
|
Q(c,c) Ú ØR(b,c). |
(5) |
"x"y (Q(x,y)ÚØR(x,y)).
Если в качестве аргумента выступает переменная, то она унифицируема с любой константой. Если в одной и той же фразе переменная встречается более одного раза и эта переменная в процессе резолюции унифицируется с константой, то резольвента будет содержать данную константу на тех местах, где рассматриваемая переменная располагалась в исходной фразе. К примеру, фразы
|
P(a) Ú ØQ(a,b) |
(6) |
|
Q(x,y) Ú R(x,y) |
(7) |
|
P(a) Ú ØR(a,b), |
(8) |
Любую формулу исчисления предикатов можно привести к конъюнктивной нормальной форме, т.е. представить в виде множества фраз.
Мутанты
Написать программу, способную производить “мутантов”, т. е. гибридов различных животных. Животные задаются их названиями в виде атомов. Два животных производят на свет мутанта, если окончание названия первого животного совпадает с началом названия второго.
Каждое животное задается с помощью факта animal(<животное>). Вы должны определить предикат mutant, вызов которого в виде цели mutant(X) сопоставит переменной X различные мутанты.
Вот результаты, полученные на множестве животных (крокодил, черепаха, карибу, лошадь, хамелеон, буйвол, волк):
крокодилошадь,
буйволк,
карибуйвол,
черепахамелеон,
волкрокодил,
волкарибу,
буйволошадь.
Нам необходимо использовать предикат name(?Атом,?Список) - конвертирование атома в список кодов ASCII. Так, например, вызов name(‘волк’,X)? конкретизирует переменную X=[162,174,171,170].
% Программа "Мутанты"
animal('крокодил').
animal('черепаха').
animal('карибу').
animal('лошадь').
animal('хамелеон').
animal('буйвол').
animal('волк').
animal(X,Y):-
animal(X),
name(X,Y).
mutant(Z):-
animal(_,X),animal(_,Y),
append(_,[BH|BT],X),
append([BH|BT],[CH|CT],Y),
append(X,[CH|CT],Z1),
name(Z,Z1).
Недостатки отсечения
Нарушается соответствие между процедурным и декларативным смыслами программы.
Пример:
p :- a, b.
p :- c.
Декларативный смысл: p <=> (a and b) or c.
p :- a, !, b.
p :- c.
Декларативный смысл: (a and b) or ( not a and c) <=> p
p :- c.
p:- a, b.
Декларативный смысл: p <=> (a and b) or c.
Негативная информация
Информация о фактах, которые не являются истинными, или об отношениях, которые не соблюдаются, называется негативной. Обычно негативная информация не хранится в Пролог-программах в явной форме. Вместо этого считается, что вся информация, отсутствующая в текущем множестве фраз (предложений) ложна. Это эквивалентно предложению о том, что всегда имеет силу следующий принцип:
Если правило P не представлено в текущей программе, то считается, что представлено отрицание P.
Ограничение перебора
В процессе достижения цели пролог-система осуществляет автоматический перебор вариантов, делая возврат при неуспехе какого-либо из них. Такой перебор - полезный программный механизм, поскольку он освобождает пользователя от необходимости программировать его самому. С другой стороны, ничем не ограниченный перебор может стать источником неэффективности программы. Поэтому иногда требуется его ограничить или исключить вовсе. Для этого в Прологе предусмотрена конструкция “отсечение”.
Рассмотрим двухступенчатую функцию.
Правило 1: если X<3, то Y=0
Правило 2: если 3£X и X<6, то Y=2
Правило 3: если 6£ X, то Y=4
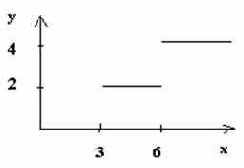
На Прологе это можно выразить с помощью бинарного отношения f(X,Y) так:
f(X,0) :- X<3.
f(X,2) :- 3 =<X,X<6.
f(X,4) :- 6=<X.
Мы проделаем с этой программой два эксперимента. Каждый из них обнаружит в ней свой источник неэффективности, и мы устраним оба этих источника по очереди, применив оператор отсечения.
· Эксперимент 1.
?- f(1,Y), 2<Y.
Три правила, входящие в отношение f, являются взаимоисключающими, поэтому успех возможен самое большое в одном из них. Следовательно, мы (но не пролог-система) знаем, что, как только успех наступил в одном из них, нет смысла проверять остальные, поскольку все равно они обречены на неудачу. О том, что в правиле 1 наступил успех, становится известно в точке, обозначенной словом “отсечение”. Для предотвращения бессмысленного перебора мы должны явно указать пролог-системе, что не нужно осуществлять возврат из этой точки.
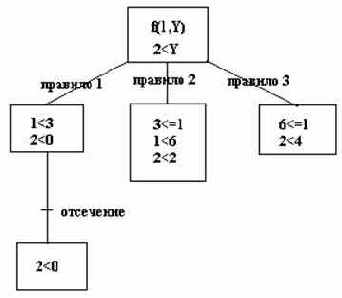
Мы можем сделать это при помощи конструкции отсечения. “Отсечение” записывается в виде символа ‘!’, который вставляется между целями и играет роль некоторой псевдоцели.
f(X,0) :- X<3,!.
f(X,2) :- 3 =< X, X<6,!.
f(x,4) :- 6 =< X.
Символ “!” предотвращает возврат из тех точек программы, в которых он поставлен. Если мы теперь спросим
?- f(1,Y),2<Y.
то пролог- система породит левую часть дерева, изображенного на рисунке. Эта ветвь потерпит неудачу на цели 2<0. Система попытается сделать возврат, но вернуться она сможет не далее точки, помеченной символом “!”. Альтернативные ветви, соответствующие правилу 2 и правилу 3, порождены не будут.
Вывод: добавив отсечения, мы повысили эффективность. Если их теперь убрать, программа породит тот же результат, только на его получение она потратит, скорее всего, больше времени. Можно сказать, что в нашем случае после введения отсечений мы изменили только процедурный смысл программы, оставив при этом её декларативный смысл в неприкосновенности.
· Эксперимент 2.
Проделаем теперь еще один эксперимент со второй версией программы. Предположим, мы задаем вопрос:
?- f(7,Y).
Y=4
Yes
Перед тем, как был получен ответ, система пробовала применить все три правила. Вначале выясняется, что X<3 не является истиной (7<3 терпит неудачу). Следующая цель 3=<X (3=<7 - успех). Но нам известно, что, если первая проверка неуспешна, то вторая обязательно будет успешной, так как второе целевое утверждение является отрицанием первого. Следовательно, вторая проверка лишняя и соответствующую цель можно опустить. То же самое верно и для цели 6=<X в правиле 3.
Теперь мы можем опустить в нашей программе те условия, которые обязательно выполняются при любом вычислении.
f(X,0) :- X<3,!.
f(X,2) :- X<6,!.
f(X,4).
Эта программа дает тот же результат, что и исходная, но более эффективна, чем обе предыдущие. Однако, что будет, если мы теперь удалим отсечения? Программа станет такой:
f(X,0) :- X<3.
f(X,2) :- X<6.
f(X,4).
?- f(1,Y).
Y=0;
Y=2;
Y=4;
No
Важно заметить, что в последней версии, в отличие от предыдущей, отсечения затрагивают не только процедурное поведение, но изменяют и декларативный смысл программы.
Назовем “целью-родителем” ту цель, которая унифицировалась с головой предложения, содержащего отсечение.
Когда в качестве цели встречается отсечение, такая цель сразу же считается успешной и при этом заставляет систему принять те альтернативы, которые были выбраны с момента активизации цели- родителя до момента, когда встретилось отсечение. Все оставшиеся в этом промежутке (от цели-родителя до отсечения) альтернативы не рассматриваются.
Пример:
H :- B1,B2,...,Bm,!,...,Bn.
Будем считать, что это предложение активизировалось, когда некоторая цель G унифицировалась с H. Тогда G является целью-родителем. В момент, когда встретилось отсечение, успех уже наступил в целях B1,...,Bm. При выполнении отсечения это (текущее) решение B1,...,Bm “замораживается” и все возможные оставшиеся альтернативы больше не рассматриваются. Далее, цель G связывается теперь с этим предложением: любая попытка сопоставить G с головой какого-либо другого предложения пресекается.
Пример:
C :- P,Q,R,!,S,T,U.
C :- V.
A :- B,C,D.
?- A.
Отсечение повлияет на вычисление цели С следующим образом. Перебор будет возможен в списке целей P,Q,R; однако, как только точка отсечения будет достигнута, все альтернативные решения для этого списка изымаются из рассмотрения. Альтернативное предложение, входящее в C
C:-V.
также не будет учитываться. Тем не менее, перебор будет возможен в списке целей S,T,U. Отсечение повлияет только на цель C. Оно будет невидимо из цели A, и автоматический перебор все равно будет происходить в списке целей B,C,D вне зависимости от наличия отсечения в предложении, которое используется для достижения C.
Олимпиадная задача
Международная олимпиада по математике, 1963 год.
Ученики A,B,C,D и E участвовали в одном конкурсе. Пытаясь угадать результаты соревнований, некто предполагал, что получится последовательность A,B,C,D,E. Но оказалось, что он не указал верно ни место какого-либо из участников и никакой пары следующей непосредственно друг за другом учеников. Некто другой, предполагая результат D,A,E,C,B, угадал правильно места двух учеников, а также две пары (непосредственно следующих друг за другом учеников).
Каков был на самом деле результат конкурса?.
% правильная расстановка участников (представленных в виде место-имя)
rezult:-
inicial(M1,M2,M3,M4,M5,[1,2,3,4,5]),
pos([M1-a,M2-b,M3-c,M4-d,M5-e],0),
para([M1-a,M2-b,M3-c,M4-d,M5-e],0),
pos([M4-d,M1-a,M5-e,M3-c,M2-b],2),
para([M4-d,M1-a,M5-e,M3-c,M2-b],2),
write(M1-a/M2-b/M3-c/M4-d/M5-e).
% инициализация переменных элементами списка
inicial(X1,X2,X3,X4,X5,L):-
member(X1,L),
select(L,X1,S2),
member(X2,S2),
select(S2,X2,S3),
member(X3,S3),
select(S3,X3,S4),
member(X4,S4),
select(S4,X4,[X5]).
% N - количество правильных мест элементов в списке L
pos(L,N):-
pos(L,N,0,1).
pos(_,N,N,6).
pos(L,N,S,I):-
I<6,
nth1(I,L,I-_),
S1 is S+1,
I1 is I+1,
pos(L,N,S1,I1).
pos(L,N,S,I):-
I<6,
nth1(I,L,J-_),
I=\=J,
I1 is I+1,
pos(L,N,S,I1).
% N - количество правильных пар непосредственно следующих друг за
% другом элементов в списке L
para(L,N):- para(L,N,0,1).
para(_,N,N,5).
para(L,N,S,I):-
I<5,
nth1(I,L,A1-_),
I1 is I+1,
nth1(I1,L,A2-_),
A2 =:= A1+1,
S1 is S+1,
para(L,N,S1,I1).
para(L,N,S,I):-
I<5,
nth1(I,L,A1-_),
I1 is I+1,
nth1(I1,L,A2-_),
A2 =\= A1+1,
para(L,N,S,I1).
?- rezult.
3 - a / 5 - b / 4 - c / 2 - d / 1 - e
Yes
Знание и мудрость обогащают человека. Знание ведет к компьютерам, а мудрость - к китайским палочкам для еды.
А. Дж. Перлис, первый лауреат премии Тьюринга, 1966 год
Особенности языка Пролог
В языке Пролог сочетается использование нескольких важных концепций, к числу которых относятся:
1) применение фраз Хорна для представления знаний;
2) дескриптивный стиль программирования;
3) как декларативная, так и процедурная семантика;
4) возможность чередовать программный текст метауровня с текстом объектного уровня.
Как логические фразы Хорна записываются на языке Пролог?
Логическая или, точнее, хорновская логическая программа состоит из набора хорновских фраз, которые в языке Пролог называются фактами и правилами. Структура этих правил и фактов такова, что, с одной стороны, с их помощью довольно естественно описываются многие задачи, а с другой стороны, они допускают простую процедурную интерпретацию. Два этих обстоятельства и позволяют использовать язык фактов и правил в качестве языка программирования.
Фактом называется формула вида
P(t1,...,tn),
где P - предикатный символ, а t1,...,tn - термы, построенные из переменных, констант и функциональных символов. С точки зрения математической логики, факты - это атомарные формулы.
Правилом называется формула вида
A1 Ù ... Ù An Þ A0 (равносильная формула A0ÚØA1Ú...ÚØAn),
где все Ai - атомарные формулы (таким образом, факт - это частный случай правила). В обозначениях Пролога эту формулу принято записывать по-иному:
A0 :- A1,A2,...,An.
Запросом к логической программе называется формула вида
A1Ù...ÙAn,
где все Ai - атомарные формулы, вместе с приглашением Пролога на ввод такой запрос записывается в виде
?- A1,A2,...,An.
Запрос, не содержащий переменных, читается так: верно ли, что A1 и ... и An? Если же в атомарных формулах запроса содержатся переменные X1,...,Xm, то его следует читать иначе: для каких объектов X1,...,Xm верно A1 и ... и An?
Мы будем использовать SWI-prolog (1994, University of Amsterdam).
Основные синтаксические объекты: атомы, константы и переменные. Константы
состоят из атомов и чисел. Числа - целые и вещественные. Атомы - обозначения для других постоянных объектов предметной области. Атомы могут изображаться тремя различными способами:
1) последовательностью латинских букв, цифр, начинающейся со строчной буквы;
2) последовательностью, состоящей из специальных символов
<---> | ==>| ... | &,
(Не используйте для обозначения атомов следующие комбинации и отдельные символы :- | , | ; | . | ! );
3) любыми последовательностями символов, заключенными в апострофы (в т.ч. и русскими буквами).
Атомы используются и для обозначения предикатных символов, некоторые предикатные символы являются встроенными. Переменные обозначаются любыми последовательностями латинских букв или цифр, начинающимися с большой буквы или символа подчеркивания.
Главным компонентом интерпретатора языка Пролог является универсальный механизм решения задач, принцип действия которого основан на правиле резолюции. Для того, чтобы воспользоваться этим механизмом, программист должен четко описать задачу при помощи фраз Хорна, выраженных на языке Пролог. В каждой фразе формулируется некоторое отношение между термами. Терм - это обозначение, представляющее некоторую сущность из исследуемого мира. Для того, чтобы привести в действие данный механизм решения задач, программист должен написать запрос, согласно которому будет необходимо выяснить, является ли конкретная атомарная формула следствием текущего множества фраз, представленных в программе.
Отрицание определяется через отсечение
not (P) :-
P, !, fail;
true.
r(a).
g(b).
p(X) :- not r(X).
?- g(X), p(X).
X = b
Yes
?- p(X), g(X).
No
Порядок целей повлиял на работу программы. В первом случае, когда вызывается подцель p(X), переменная X уже конкретизована значением b. Во втором случае p(X) вызывается со свободной переменной.
Что касается трудностей Пролога, то подобное возникает и в других языках.
Отрицание в явной форме
Встроенный предикат not (“не”) имеет один аргумент. Этим аргументом является цель, значение истинности которой (после обработки данного запроса) заменяется противоположным. Если запрос успешен, то отрицание этой цели (запроса) является неудачей и, наоборот, если запрос терпит неудачу, то его отрицание будет успехом. Запрос
?- not(отец (питер, X).
будет истинным тогда и только тогда, когда
?- отец (питер, X )
потерпит неудачу.
Переменные в цели с предикатом not квантифицированы универсальным образом (т. е. используется квантор всеобщности).
Пример.
Напишем правило, определяющее сельского жителя как человека, который не является ни горожанином, ни жителем пригорода.
горожанин(джек).
житель_пригорода(сюзан).
сельский_ житель(X):-
not(горожанин(X)),
not(житель_ пригорода(X)).
?- сельский_житель (билл).
Yes.
Всякая точная наука основывается на приблизительности.
Бертран Рассел
Порядок предложений и целей
Логически непротиворечивое определение предиката может быть процедурно неправильно. Вызов
?- p.
предиката, определенного правилом
p :- p,
приводит к бесконечному циклу.
Рассмотрим различные варианты программы "родственные отношения", полученные путем переупорядочивания предложений и целей.
parent(pam,bob).
parent(tom,bob).
parent(tom,lis).
parent(bob,ann).
parent(bob,pat).
parent(pat,jim).
Вариант 1.
predok(X,Y) :-
parent(X,Y).
predok(X,Y) :-
parent(X,Z),
predok(Z,Y).
Трассировка запроса:
?- predok (tom,pat)
дает следующую последовательность выполнения.
Call: ( 7) parent(tom, pat)
Fail: ( 7) parent(tom, pat)
Call: ( 7) parent(tom, L384), predok(L384, pat)
Call: ( 8) parent(tom, L384)
Exit: ( 8) parent(tom, bob)
Call: ( 9) parent(bob, pat)
Exit: ( 9) parent(bob, pat)
Exit: ( 7) parent(tom, bob), predoc(bob, pat)
Yes
Вариант 2.
pred2(X,Z):-
parent(X,Y),
pred2(Y,Z).
pred2(X,Z):-
parent(X,Z).
Трассировка запроса:
?- pred2 (tom,pat)
показывает более продолжительную последовательность выполнения.
Call: ( 7) parent(tom, L384),predok(L384, pat)
Call: ( 8) parent(tom, L384)
Exit: ( 8) parent(tom, bob)
Call: ( 9) parent(bob, L520), predok(L520, pat)
Call: ( 10) parent(bob, L520)
Exit: ( 10) parent(bob, ann)
Call: ( 11) parent(ann, L656), predok(L656, pat)
Call: ( 12) parent(ann, L656)
Fail: ( 12) parent(ann, L656)
Fail: ( 11) parent(ann, L656), predok(L656, pat)
Call: ( 11) parent(ann, pat)
Fail: ( 11) parent(ann, pat)
Exit: ( 10) parent(bob, pat)
Call: ( 11) parent(pat, L612), predok(L612, pat)
Call: ( 12) parent(pat, L612)
Exit: ( 12) parent(pat, jim)
Call: ( 13) parent(jim, L704), predok(L704, pat)
Call: ( 14) parent(jim, L704)
Fail: ( 14) parent(jim, L704)
Fail: ( 13) parent(jim, L704) ,predok(L704, pat)
Call: ( 13) parent(jim, pat)
Fail: ( 13) parent(jim, pat)
Fail: ( 11) parent(pat, L612), predok(L612, pat)
Call: ( 11) parent(pat, pat)
Fail: ( 11) parent(pat, pat)
Fail: ( 9) parent(bob, L520) , predok(L520, pat)
Call: ( 9) parent(bob, pat)
Exit: ( 9) parent(bob, pat)
Exit: ( 7) parent(tom, bob, pat)
Yes
Программа работает правильно, но не эффективно.
Вариант 3.
pred3(X,Z):-
parent(X,Z).
pred3(X,Z):-
pred3(X,Y),
parent(Y,Z).
Этот вызов благополучно вычисляется
?- pred3(tom,pat).
Call: ( 7) parent(tom, pat)
Fail: ( 7) parent(tom, pat)
Call: ( 7) predok(tom, L384), parent(L384, pat)
Call: ( 9) parent(tom, L384)
Exit: ( 9) parent(tom, bob)
Call: ( 8) parent(bob, pat)
Exit: ( 8) parent(bob, pat)
Exit: ( 7) predok(tom, bob), parent(bob, pat)
Yes
Повтор, определяемый пользователем
repeat.
repeat:-
repeat.
С помощью предиката repeat можно устроить цикл типа "до тех пор, пока".
repetive:-
repeat,
<повторяемое тело цикла>,
<условие выхода>, !.
Пример. Программа “Эхо” считывает терм, введенный с клавиатуры, и дублирует его на экран, если пользователь введет stop, то программа завершается.
do-echo:-
repeat,
read(Term),
write_ln(Term),
check(Term),!.
check(stop):-
write_ln(' - OK,bye').
check(_):-
fail.
Повторение и откат
repetive:-
<предикаты>,
fail.
Встроенный предикат fail (неудача) вызывает возврат (откат), так что предикаты выполняются еще раз.
Пример:
parent(pam,bob).
parent(tom,bob).
parent(tom,lis).
parent(bob,ann).
parent(bob,pat).
parent(pat,jim).
Как распечатать все пары?
everybody:-
parent(X,Y),
write(X),write(' есть родитель '),write_ln(Y),
fail.
everybody.
?- everybody.
pam есть родитель bob
tom есть родитель bob
tom есть родитель lis
bob есть родитель ann
bob есть родитель pat
pat есть родитель jim
Yes
Предположение о замкнутости мира
С практической точки зрения это означает, что интерпретатор не может отличить неизвестное предложение от доказуемо неистинного предложения. Принцип, приведенный выше, известен как предположение о замкнутости мира. Множество предложений текущей программы называется миром. Это - замкнутый мир, поскольку интерпретатор ведет себя так, как будто бы в этом мире содержатся все возможные знания.
Предположение об открытости мира
При работе с неизвестной информацией, альтернативой предложению о замкнутости мира, служит предположение об открытости мира:
Если правило P отсутствует в текущей программе, то считается, что P ни истинна, ни ложна.
В соответствии с предположением об открытости мира запрос может обладать одним из трех допустимых истинностных значений: истина, ложь или неизвестно. Если запрос признан неизвестным, то программа может предпринять какие-то особые действия, скажем, она может обратиться к альтернативному источнику знаний. По умолчанию интерпретатор языка Пролог руководствуется предположением о замкнутости мира. Поэтому, если требуется, чтобы поведение программы соответствовало предположению об открытости мира, то это нужно выражать в явном виде при составлении программы. Составление такой программы равнозначно изменению неявного предиката метаязыка, описывающего смысл запроса.
Пример процедуры, поведение которой соответствует предположению об открытости мира.
Программа содержит позитивные факты
father(tom,bob).
father(bob,pat).
Явно заданы негативные факты в виде
false(father(pat,_)).
Если нельзя доказать, что утверждение истинно или ложно, то оно считается неизвестным.
prove(P) :-
P,
write_ln('=> истино'),!.
prove(P) :-
false(P),
write_ln('=>ложно'),!.
prove(P):-
not(P),
not(false(P)),
write_ln('=>неизвестно').
?- prove(father(pat,jim)).
=>ложно
Yes
?- prove(father(jim,X)).
=>неизвестно
X = G836
Yes
?- prove(father(X,bob)).
=> истино
X = tom
Yes
Преимущества отсечения
При помощи отсечения часто можно повысить эффективность программы. Идея состоит в том, чтобы прямо сказать пролог-системе: не пробуй остальные альтернативы, так как они все равно обречены на неудачу.
Применяя отсечение, можно описать взаимоисключающие правила, например, с помощью условной конструкции. Выразительность языка при этом повышается.
Применение метода резолюций для ответов на вопросы
Предположим, что у нас есть предикат F(x,y), означающий, что x - отец y, и истинна следующая формула
F(john,harry) Ù F(john,sid) Ù F(sid,liz).
Таким образом, у нас есть три дизъюнкта. Они не содержат переменных или импликаций, а просто представляют базисные факты.
Введем еще три предиката M(x), S(x,y) и B(x,y), означающие соответственно, что x - мужчина, что он единокровен с y, что он брат y. Мы можем записать следующие аксиомы о семейных отношениях.
"x,y (F(x,y) Þ M(x))
"x,y,w (F(x,y) Ù F(x,w) Þ S(y,w))
"x,y (S(x,y) Ù M(x) Þ B(x,y))
Они утверждают следующее: 1) все отцы - мужчины; 2) если у детей один отец, то они единокровны; 3) брат - это единокровный мужчина.
Пусть мы задали вопрос $z B(z,harry)? Чтобы найти ответ с помощью метода резолюции, мы записываем отрицание вопроса "z ØB(z,harry). Затем приводим аксиомы к нормальной форме и записываем каждый дизъюнкт в отдельной строке (так как каждый дизъюнкт истинен сам по себе):
| ØF(x,y) Ú M(x) | (1) | ||
| ØF(x,y) Ú ØF(x,w) Ú S(y,w) | (2) | ||
| ØS(x,y) Ú ØM(x) Ú B(x,y) | (3) | ||
| F(john,harry) | (4) | ||
| F(john,sid) | (5) | ||
| F(sid,liz) | (6) | ||
| ØB(z,harry) | (7) |
Мы не пишем внешних кванторов всеобщности, так как подразумевается, что каждая переменная связана таким квантором.
Для применения резолюции необходимо найти для данной пары дизъюнктов такую подстановку термов вместо переменных, чтобы после нее некоторый литерал одного из дизъюнктов стал отличаться от некоторого литерала другого дизъюнкта лишь отрицанием. Мы можем делать подстановки, так как все переменные связаны кванторами всеобщности. Если, например, мы подставим john вместо x и sid вместо y, то получим следующее:
ØF(john,sid) Ú ØF(john,w) Ú S(sid,w).
Мы можем применить правило резолюции к этому дизъюнкту и (5), что дает новый дизъюнкт:
| ØF(john,w) Ú S(sid,w)
из (5) и (2) {x->john,y->sid} | (8) |
Продолжая, получим
|
S(sid,harry) из (4) и (8) {w->harry} |
(9) |
|
M(sid) из (6) и (1) {x->sid,y->liz} |
(10) |
|
ØS(sid,y) Ú B(sid,y) из (10) и (3) {x->sid} |
(11) |
|
B(sid,harry) из (9) и (11) {y->harry} |
(12) |
|
пустой дизъюнкт из (12) и (7) {z->sid} |
2. ВВЕДЕНИЕ В ЯЗЫК ПРОЛОГ
"… инструменты, которые мы пытаемся использовать, а также язык (язык программирования в том числе) или обозначения, применяемые нами для выражения или записи наших мыслей, являются главными факторами, определяющими нашу способность хоть что-то думать или выражать!"
Из лекции лауреата премии Тьюринга за 1972 год Э. Дейкстры.
Пролог-программы: родственные отношения
Сущности предметной области – люди. Предикат parent(X,Y) обозначает бинарное отношение "X родитель Y".
parent(pam,bob).
parent(tom,bob).
parent(tom,liz).
parent(bob,ann).
parent(bob,pat).
parent(pat,john).
Диалог с интерпретатором:
?- parent(bob,pat).
Yes
?- parent(liz,pat).
No
?- parent(tom,sid).
No
?- parent(X,liz).
X = tom
Yes
?- parent(bob,X).
X = ann
Yes
Вводя ";" после ответа Пролога (вместо Enter), мы заставляем интерпретатор продолжить поиск ответа.
?- parent(bob,X).
X = ann ;
X = pat ;
No
?- parent(X,Y).
X = pam
Y = bob ;
X = tom
Y = bob ;
X = tom
Y = liz ;
X = bob
Y = ann ;
X = bob
Y = pat ;
X = pat
Y = john ;
No
Кто является родителем родителя Джона?
?- parent(Y,john),parent(X,Y).
X = bob
Y = pat
Yes
Кто внуки Тома?
?- parent(tom,X),parent(X,Y).
X = bob
Y = ann ;
X = bob
Y = pat ;
No
Использование анонимных переменных ("_").
Кто имеет детей?
?- parent(X,_).
X = pam ;
X = tom ;
X = tom ;
X = bob ;
X = bob ;
X = pat ;
No
Добавим теперь в нашу программу-пример еще несколько родственных отношений. Предикат women(X) обозначает свойство "X – женщина". Предикат mother(X,Y) обозначает отношение "X – мать Y".
women(pam).
women(liz).
women(ann).
women(pat).
mother(X,Y):-
women(X),
parent(X,Y).
?- mother(X,Y).
X = pam
Y = bob ;
X = pat
Y = john ;
No
Рекурсивное определение правил.
Предикат predok(X,Y) обозначает отношение "X – предок Y".
predok(X,Y) :-
parent(X,Y).
predok(X,Y) :-
parent(X,Z),
predok(Z,Y).
?- predok(X,john).
X = pat ;
X = pam ;
X = tom ;
X = bob ;
No
Факты существуют только там, где отсутствуют люди. Когда люди появляются, остаются одни интерпретации.
Станислав Лем. Расследование
ы использования структур
Сортировка списка с использованием дерева
% tree_sort(+X,-Y)
% X - исходный список, результат Y - упорядоченный список
tree_sort(X,Y):-
make_tree(X,Z),
flat(Z,Y).
% make_tree(+X, -Y) - создание упорядоченного дерева Y из списка X
make_tree([],nil).
make_tree([H|T],Z):-
make_tree(T,Y),
insert(H,Y,Z).
% insert(+N,+X,-Y) - вставка элемента N в упорядоченное дерево X
insert(N,nil,tree(nil,N,nil)).
insert(N,tree(L,Root,R),tree(L1,Root,R)):-
N =< Root,
insert(N,L,L1).
insert(N,tree(L,Root,R),tree(L,Root,R1)):-
N > Root,
insert(N,R,R1).
% flat(+X,-Y) - разглаживание дерева X в список Y
flat(nil,[]).
flat(tree(L,N,R),Z):-
flat(L,L1),
flat(R,R1),
append(L1,[N|R1],Z).
?- make_tree([8,10,6,5],X).
X = tree(nil, 5, tree(nil, 6, tree(tree(nil, 8, nil), 10, nil)))
Yes
Дифференцирование
Задача. Написать предикат dv(+Term,+Atom,-Term2), где Term2 есть результат дифференцирования Term1 по математической переменной Atom. Term1 - арифметическое выражение, составленное из атомов и чисел с использованием скобок, знаков операций +, -, *, /, ^ и функций sin(x), cos(x), ln(x) и e^x.
Логическая программа дифференцирования - просто набор соответствующих правил дифференцирования.
dv(X,X,1).
dv(Y,_,0):-
number(Y).
dv(Y,X,0):-
atom(Y),
X \= Y.
dv(X^N,X,N*X^(N-1)):-
number(N).
dv(sin(X),X,cos(X)).
dv(cos(X),X,-sin(X)).
dv(e^X,X,e^X).
dv(ln(X),X,1/X).
dv(Y+Z,X,(DY+DZ)):-
dv(Y,X,DY),
dv(Z,X,DZ).
dv(Y-Z,X,(DY-DZ)):-
dv(Y,X,DY),
dv(Z,X,DZ).
dv(Y*Z,X,DY*Z+DZ*Y):-
dv(Y,X,DY),
dv(Z,X,DZ).
dv(Y/Z,X,(DZ*Y-DY*Z)/Z*Z):-
dv(Y,X,DY),
dv(Z,X,DZ).
Правило дифференцирования сложной функции представляет собой более тонкий случай. В правиле утверждается, что производная от f(g(x)) по x есть производная f(g(x)) по g(x), умноженная на производную g(x) по x.
В данной форме правило использует квантор по функциям и находится вне области логического программирования, рассматриваемого нами. Нам понадобится встроенный предикат =../2.
?Term =.. ?List
List есть список, голова которого есть функтор терма Term и остальные элементы суть аргументы терма. Каждый из аргументов может быть переменной, но не оба сразу. Этот предикат называется `Univ'.
?- foo(hello, X) =.. List.
List = [foo, hello, X]
?- Term =.. [baz, foo(1)]
Term = baz(foo(1))
Использование предиката univ позволяет изящно задать правило дифференцирования сложных функций.
dv(F_G_X,X,DF*DG):-
F_G_X =.. [_,G_X],
dv(F_G_X,G_X,DF),
dv(G_X,X,DG).
Предикат dv выдает результат дифференцирования в неупрощенном виде.
?-dv(3*y+a,y,D).
D = 3*1 +0*y +0
Yes
Последовательность одинакова плоха и для ума и для тела. Последовательность чужда человеческой природе, чужда жизни. До конца последовательны только мертвецы.
Олдос Хаксли
Процедура проверки принадлежности списку, дающая единственное решение
Обычное поведение:
member(X, [X|L]).
member(X, [Y|L]):-
member(X, L).
?- member(X,[1, 2, 1, 2]).
X=1;
X=2;
X=1;
X=2;
No
С отсечением:
member(X, [X|L]):- !.
member(X, [Y |L]):-
member(X, L).
?- member(X, [1, 2, 1, 2]).
X=1;
No
?- member(X, [1,2,5,7]), X>3.
No
Программирование второго порядка
Программирование на Прологе расширяется введением методов, отсутствующих в модели логического программирования. Эти методы основаны на свойствах языка, выходящих за рамки логики первого порядка. Они названы методами второго порядка, поскольку речь здесь идет о множествах и их свойствах, а не об отдельных элементах. Кроме того, применения ламбда-выражений и предикатных переменных позволяют рассматривать функции и отношения как “первоклассные” объекты данных.
findall(+Var, +Goal, -Bag)
Создает список всех конкретизаций переменной Var, полученных при бэктрекинге при выполнении цели Goal, и унифицирует результат с Bag. Bag - пустой список, когда Goal не имеет решения.
?- findall(X,(member(X,[1,2,3,4,5]),0 is X mod 2),L).
X = G1564
L = [2,4]
Yes
Логика первого порядка позволяет проводить квантификацию по отдельным элементам. Логика второго порядка, кроме того, позволяет проводить квантификацию по предикатам. Включение такого расширения в логическое программирование влечет за собой использование правил с целями, предикатные имена которых являются переменными. Имена предикатов допускают обработку и модификацию.
apply(+Term, +List)
Присоединяет элементы списка List к аргументам терма Term и вызывает полученный терм в качестве цели. Например, `apply(plus(1),[2, X])' вызывает `plus(1, 2, X)'.
?- apply(plus,[1,2,X]).
X = 3 ;
No
?- apply(is,[X,4*6*(3+2)]).
X = 120
Yes
?- apply(=,[X,a*6*(x+2)]).
X = a * 6 * (x + 2)
Yes
?- apply(=(X),[a*6*(x+2)]).
X = a * 6 * (x + 2)
Yes
?- apply(append,[[1,2,3],[6,7,8],X]).
X = [1,2,3,6,7,8]
Yes
checklist(+Pred, +List)
Проверяет все ли элементы списка List удовлетворяют предикату Pred.
?- checklist(number,[1,4,8.9,5/7]).
No
?- checklist(number,[1,4,8.9]).
Yes
?- [user].
| p(2).
| p(3).
| p(5).
| p(7).
| user compiled, 52.34 sec, 388 bytes.
Yes
?- checklist(p,[2,5,2,7]).
Yes
?- checklist(p,[2,5,2,1]).
No
Этой ужасной минуты я не забуду никогда в жизни! – сказал Король.
Забудешь – заметила Королева, - если не запишешь в записную книжку.
Льюис Кэрролл. Алиса в Зазеркалье
7.5. Запоминающие функции
Запоминающие функции сохраняют промежуточные результаты с целью их использования в дальнейших вычислениях. Запоминание промежуточных результатов в чистом Прологе невозможно, поэтому реализация запоминающих функций основана на побочных эффектах.
Исходной запоминающей функцией является предикат lemma(Goal). Операционное понимание состоит в следующем: предпринимается попытка доказать цель Goal, и если попытка удалась, результат доказательства сохраняется в виде леммы. Отношение задается следующим образом:
lemma(P) :- P, asserta((P :- !)).
Следующая попытка доказать цель P приведет к применению нового правила, что позволяет избежать ненужного повторения вычислений. Отсечение введено для того, чтобы воспрепятствовать повторному рассмотрению всей программы. Применение отсечения обосновано лишь в тех случаях, когда цель P имеет не более одного решения.
Использование лемм демонстрируем на примере программы, вычисляющей функцию Аккермана:
f(0,n) = n+1
f(m,0) = f(m-1,1) если m>0
f(m,n) = f(m-1,f(m,n-1)) если m,n>0
Факт do будем использовать в качестве глобального счетчика
для подсчета вызовов функции ackerman, предикат без аргументов inc увеличивает значение счетчика на 1.
ackerman(0,N,N1):-
inc,
N1 is N+1.
ackerman(M,0,Val):-
M>0,
inc,
M1 is M-1,
ackerman(M1,1,Val).
ackerman(M,N,Val):-
M>0,N>0,
inc,
N1 is N-1,
ackerman(M,N1,Val1),
M1 is M-1,
ackerman(M1,Val1,Val).
inc:-
do(X),
X1 is X+1,
retract(do(_)),
assert(do(X1)).
do(0).
?- ackerman(3,2,X),do(Y).
X = 29
Y = 541
Yes
Теперь приведем вариант с запоминающей функцией.
ackerman(0,N,N1):-
inc,
N1 is N+1.
ackerman(M,0,Val):-
M>0,
inc,
M1 is M-1,
lemma(ackerman(M1,1,Val)).
ackerman(M,N,Val):-
M>0,N>0,
inc,
N1 is N-1,
lemma(ackerman(M,N1,Val1)),
M1 is M-1,
lemma(ackerman(M1,Val1,Val)).
lemma(P):-
P,
asserta((P:-!)).
do(0).
?- ackerman(3,2,X),do(Y).
X = 29
Y = 73
Yes
8. МОДИФИКАЦИЯ СИНТАКСИСА (ОПЕРАТОРНАЯ ЗАПИСЬ)
Прологовские операторы суть имена функций и/или предикатов (унарных и/или бинарных), записанных до, после или между аргументами, им свойственны приоритет или ассоциативность:
?- a+b+c = X+Y.
X = a + b
Y = c
Yes
?- a+b*c = X+Y.
X = a
Y = b * c
Yes
?- -a+b+c = X+Y.
X = -a + b
Y = c
Yes
В данных примерах встроенными операторами являются предикат = и функторы +,- и *, но программист может ввести собственные операторы.
Атрибутика оператора:
* предшествование, выраженное натуральным числом (от 0 до 1200): чем больше предшествование, тем меньше приоритет;
* позиция - инфиксная, префиксная или постфиксная;
* ассоциативность.
Предшествование выражают числом, а позицию и ассоциативность - одним из следующих способов:
* префиксность оператора (точнее, префиксная запись оператора): fx или fy;
* постфиксность оператора: xf или yf;
* инфиксность оператора: xfx,xfy,yfx или yfy.
Здесь f - оператор, x и y - операнды:
* запись yfx означает левую ассоциативность
a f b f c f d º ((a f b) f c) f d,
+ и * обладают левой ассоциативностью;
* запись xfy означает правую ассоциативность
a f b f c º a f(b f c),
^ обладает правой ассоциативностью;
* запись x f x говорит, что оператор не обладает ассоциативностью; например, mod, поэтому X is 120 mod 50 mod 2 - синтаксическая ошибка.
Предшествование терма
Если терм заключен в скобки или не является составным, то его предшествование равно 0.
Предшествование структурного терма равно предшествованию его главного функтора.
* Операнд y означает, что “предшествование этого операнда не больше, чем предшествование оператора”.
* Операнд x означает, что “предшествование этого операнда строго меньше, чем предшествование оператора”.
Одноместный минус “-” описан как fx, поэтому --x - синтаксически неправильная запись. С другой стороны, not описан как fy, поэтому not not x - правильно.
Предикат op/3 служит для определения новых операторов и используется как директива компилятору в загружаемой программе:
:- op(+Предшествование,+Тип,+Имя)
В качестве имени может использоваться атом или список атомов, в этом случае оператор именуется различными эквивалентными именами. Предшествование, равное 0, удаляет уже сушествующую декларацию.
Наиболее важный критерий для определения оператора - это удобство чтения программы.
Пример:
:- op(750,xfx,’знает’).
Теперь факты 'знает' можно представлять в программе в инфиксной форме:
‘джейн’ ‘знает’ ‘бетти’.
‘сюзан’ ‘знает’ ‘мэри’.
?- X ‘знает’ ‘мэри’.
X=‘сюзан’
Yes
?- X=and(a,b),op(500,yfx,and).
X = a and b
Yes
?-Y=fact(a),op(700,xf,fact).
Y = a fact
Yes
Имена функций and и fact стали операторами: первый из них - бинарным, второй - унарным постфиксным. Последний раз напоминаем, что речь идет лишь о синтаксисе.
Ни с одним оператором при определении не связывается каких-либо действий над данными.
Некоторые из встроенных операторов показаны в таблице. Все эти операторы можно переопределить.
1200 xfx -->, :-
1200 fx :-, ?-
1150 fx dynamic, multifile, discontiguous
1100 xfy ;, |
1050 xfy ->
1000 xfy ,
954 xfy \\
900 fy \+, not
700 xfx <, =, =.., =@=, =:=, =<, ==, =\=, >,
>=, @<, @=<, @>, @>=, \=, \==, is
600 xfy :
500 yfx +, -, /\, \/, xor
500 fx +, -, ?, \
400 yfx *, /, //, <<, >>
300 xfx mod
200 xfy ^
Первым результатом от преподавания методологии [программирования] – а не распространения знаний – является увеличение способностей уже способных, тем самым увеличивается разброс интеллектуальных возможностей.
Из лекции лауреата премии Тьюринга 1972 г. Э. Дейкстры
Рекомендуемая литература
1. Стерлинг Л., Шапиро Э. Искусство программирования на языке Пролог. - М.: Мир, 1990.-235 с.
2. Братко И. Программирование на языке Пролог для искусственного интеллекта. - М.: Мир, 1990.-560 с.
… Но труды учения нужны не только для того, чтобы добыть известный информационный капитал. Они играют и другую роль, не зависящую от природы этого капитала: они пробуждают страсть к соревнованию, учат преодолевать препятствия, укрепляют "сопротивление стрессам" и таким образом формируют структуру личности.
Станислав Лем. Сумма технологии
Списки
Для представления списков произвольной длины используется специальная рекурсивная структура “./2” . Первый аргумент - терм любого вида; второй аргумент - другая структура “./2” или пустой список, обозначаемый [].
Список из одного элемента - атома a:
.(a,[]),
список из трех элементов a, b и c:
.(a,.(b,.(c,[]))).
Эквивалентная форма представления списков:
[a]
[a,b,c]
[[a,b],[a,b,c],[]]
Представление списков произвольной длины ³ 2:
.(one,.(two,X))
[one,two|X]
Символ "|" разделяет список на две части: начало списка и остаток списка; если начало списка состоит из одного элемента, то части называются голова списка и хвост списка. Если H - голова списка, а T - хвост, то список представляется термом [H|T].
Примеры унификации списков:
| Список 1 | Список 2 | Конкретизация переменных | |||
| [X,Y,Z] | [‘орел’,’курица’,’утка’] | X=‘орел’, Y=‘ курица’,
Z= ‘утка’ | |||
| [7] | [X|Y] | X=7, Y=[] | |||
| [1,2,3,4] | [X,Y|Z] | X=1, Y=2, Z=[3,4] | |||
| [1,2] | [3|X] | нет унификации | |||
| [1|[2]] | [X|Y] | X=1, Y=[2] |
Некоторые предикаты со списками
member(?Elem, ?List)
Отношение выполнено, когда Elem может быть унифицирован с одним из членов списка List.
member(A, [A|B]).
member(A, [B|C]) :-
member(A, C).
?- member(1,[3,4,1]).
Yes
?- member(1,[[1]]).
No
?- member(X,[a,b,[c,d],[]]).
X = a ;
X = b ;
X = [c,d] ;
X = [] ;
No
?- member(5,[X,Y|Z]).
X = 5
Y = G772
Z = G776 ;
X = G760
Y = 5
Z = G776 ;
X = G760
Y = G772
Z = [5|G1240]
Yes
append(?List1, ?List2, ?List3)
Отношение выполнено, когда список List3 унифицируется с конкатенацией списков List1 и List2.
append([], A, A).
append([A|B], C, [A|D]) :-
append(B, C, D).
?- append([a,b],[c,d],[a,b,c,d]).
Yes
?- append([a,b],[c,d],[a,b,a,c,d]).
No
?- append([8,7,6],[1,2,3],L).
L = [8,7,6,1,2,3]
Yes
Предикат append позволяет также расщеплять список на два подсписка.
?- append(L1,L2,[a,b,c]).
L2 = [a,b,c]
L1 = [] ;
L2 = [b,c]
L1 = [a] ;
L2 = [c]
L1 = [a,b] ;
L2 = []
L1 = [a,b,c] ;
No
?- append(L1,[a,b],[c,a,b]).
L1 = [c]
Yes
?- append(L1,[a,b],L3).
L3 = [a,b]
L1 = [] ;
L3 = [G1292,a,b]
L1 = [G1292]
Yes
?- append(L1,L2,L3).
L2 = G740
L3 = G740
L1 = [] ;
L2 = G740
L3 = [G1112|G740]
L1 = [G1112]
Yes
Новое определение member
member1(X,L):-
append(_,[X|_],L).
Это определение имеет очевидный декларативный смысл.
Добавить элемент спереди к списку
‘добавить’(X,L,[X|L]).
select(?List1, ?Elem, ?List2)
Селектирует элемент списка List1, который унифицируется с Elem. List2 унифицируется со списком, получаемым из List1 после удаления выбранного элемента. Обычно используется шаблон +List1, -Elem, -List2, но может также использоваться для вставки элемента в список по шаблону
-List1, +Elem, +List2.
select([A|B], A, B).
select([A|B], C, [A|D]) :-
select(B, C, D).
?- select([a,b,c],X,Y).
X = a
Y = [b,c] ;
X = b
Y = [a,c] ;
X = c
Y = [a,b] ;
No
?- select([a,b,c],b,X).
X = [a,c]
Yes
?- select(X,a,[b,c,d]).
X = [a,b,c,d] ;
X = [b,a,c,d] ;
X = [b,c,a,d] ;
X = [b,c,d,a] ;
No
Еще один вариант member
member2(X,L):-
select(L,X,_).
delete(+List1, ?Elem, ?List2)
Удаляет все элементы списка List1, что унифицируются с Elem и одновременно унифицирует результат с List2.
?- delete([a,b,a,c,a],a,X).
X = [b,c] ;
No
Структуры
В соответствии с теорией предикатов первого порядка единственная структура данных в логических программах - термы. Определение термов индуктивно. Константы и переменные являются термами. Кроме того, термами являются составные термы, или структуры. Составной терм содержит функтор (называемый главным функтором терма) и последовательность из одного или более аргументов, являющихся термами. Функтор
задается своим функциональным именем, которое суть атом, и своей арностью
(местностью), или числом аргументов. Синтаксически составные термы имеют вид f(t1,t2,...,tn), где f - имя n-арного функтора, а ti - аргументы. Геометрически мы можем рассматривать термы как деревья, где для составного терма корнем является главный функтор терма, а поддеревьями - его аргументы.
Поскольку предикаты синтаксически выглядят так же, как составные термы (роль функтора играет предикатный символ), то, следовательно, программы и данные в Прологе имеют одинаковую форму (как в Лиспе).
В Пролог-программах допускается использование одного и того же предикатного (или функционального символа) с разным числом аргументов. Это возможно, поскольку каждый функтор определяется двумя параметрами: именем и арностью.
Некоторые функциональные символы являются встроенными: например, знаки арифметических операций. Поэтому арифметические выражения, рассмотренные ранее, являются примером составных термов (структур), записанных в инфиксной форме. Но их можно записывать и в префиксной форме.
Примеры:
?- X is *(+(5,4),+(5,8)).
X = 117
Yes
?- X = *(+(5,4),+(5,8)).
X = (5 + 4) * (5 + 8)
Yes
Структуры используются в Прологе для конструирования сложных типов данных. Например, для представления даты естественно использовать терм вида ‘дата’(1,’май’,1998).
Проверка типа терма
Для проверки типа терма используются встроенные предикаты.
var(+Term) - свободная переменная
nonvar(+Term) - несвободная (конкретизированная) переменная
integer(+Term) - целое число
float(+Term) - вещественное число
number(+Term) - целое или вещественное число
atom(+Term) - атом
atomic(+Term) - атом или число
ground(+Term) -терм не содержит свободных переменных
Если не var(X) и не atomic(X), то X - структура.
Рекурсивные структуры
Рассмотрим использование рекурсивных структур при представлении простых электрических цепей. Пусть цепи содержат только резисторы, соединенные последовательно или параллельно.
Цепь, состоящую из одного резистора, будем представлять числом - номиналом резистора. Два резистора R1 и R2, соединенные последовательно, обозначим термом succ(R1,R2), а параллельно - термом para(R1,R2). Используя эти обозначения рекурсивно, мы можем определить произвольные цепи, состоящие только из последовательно и параллельно соединенных сопротивлений. Например, цепь из 4 резисторов:
para(1.0,succ(para(2.0,3.0),4.0)).
Упрощение цепей
simple(X,X):-
number(X).
simple(succ(X,Y),Z):-
simple(X,R1),
simple(Y,R2),
Z is R1+R2.
simple(para(X,Y),Z):-
simple(X,R1),
simple(Y,R2),
Z is (R1*R2)/(R1+R2).
?- simple(para(1.0,succ(para(2.0,3.0),4.0)),X).
X = 0.838710
Yes
Бинарные деревья
Бинарные деревья задаются с помощью тернарного функтора tree(Left,Root,Right), где Root - элемент, находящийся в вершине, а Left и Right - соответственно левое и правое поддерево. Пустое дерево изображается атомом nil. Следующий терм является примером более сложного дерева tree(nil, 5, tree(nil, 6, tree(tree(nil, 8, nil), 10, nil))).
% tree_member(+Element,+Tree)
% Отношение выполнено, если элемент является одной из вершин дерева
tree_member(X,tree(_,X,_)).
tree_member(X,tree(Left,_,_)):-
tree_member(X,Left).
tree_member(X,tree(_,_,Right)):-
tree_member(X,Right).
Тогда и только тогда, когда
Вследствие того, что предполагается замкнутость мира, множество предложений, определяющих отношение, имеет металингвистический смысл, несколько отличающийся от его смысла с позиций объектного языка. Предположим, к примеру, что в программе представлено три предложения:
начальник(джордж).
начальник(гарри).
начальник(нэнси).
На уровне объектного языка смысл этих фраз следующий:
“X является начальником , если
X - это джордж или
X - это гарри или
X - это нэнси”.
Однако из-за предположения замкнутости мира фактический смысл этих трех фраз на уровне метаязыка будет несколько иным:
“X является начальником тогда и только тогда, когда
X - это джордж или
X - это гарри или
X - это нэнси”.
система может пытаться решить задачу
pred4(X,Z):-
pred4(X,Y),
parent(Y,Z).
pred4(X,Z):-
parent(Y,Z).
?- pred4(tom,pat).
==> бесконечный цикл
Данный пример показывает, как пролог- система может пытаться решить задачу таким способом, при котором решение никогда не будет достигнуто, хотя оно существует. Такая ситуация не является редкостью при программировании на Прологе (как и на других языках).
Рекомендации:
1) в первую очередь применяйте самое простое правило;
2) избегайте левой рекурсии.
ВВЕДЕНИЕ В ЛОГИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
Логическое программирование является, пожалуй, наиболее впечатляющим примером применения идей и методов математической логики (точнее, одного из ее разделов - теории логического вывода) в программировании.
По миру распространяется огромное число лживых историй, и хуже всего то, что добрая половина из них – правда.
Уинстон Черчилль
Вычисление максимума
Без отсечения:
max (X,Y,X):-
X>=Y.
max(X,Y,Y):-
X =< Y.
С отсечением:
max(X,Y,X):-
X>=Y,!.
max(X,Y,Y).
Загрузка базы данных (файла с программой)
Передавать программы пролог-системе (загружать, “консультировать”) можно при помощи встроенного предиката:
consult(+File)
Все предложения программы, содержащиеся в файле, будут использованы Пролог-системой; аргумент предиката может быть списком файлов, в этом случае файлы загружаются по очереди.
Возможна и сокращенная запись для чтения программ из файлов. Файлы, из которых предстоит чтение, просто помещаются в список и этот список используется в качестве цели. Например:
?- [файл1, файл2, файл3].
Если в файле есть предложения, касающиеся отношений, которые уже были определены ранее, старые определения заменяются новыми из файла. Для того, чтобы разные предложения для одного и того же предиката из разных файлов дополняли друг друга, а не переопределяли, необходимо использовать директиву multifile в виде:
:- multifile +Functor/+Arity, ...